Что такое вайб-кодинг
Этим новомодным термином (а появился он только в 2025 году) обозначают способ программирования с помощью систем искусственного интеллекта. Машины делают машины — какое извращение! Программный код генерирует программа! На человеке же остается исходная постановка задачи, запуск кода и итеративная отладка тем же путем — уточнением задачи для ИИ.
В качестве «ИИ-программиста» можно использовать любой ИИ-ассистент, правда, качество кода у разных систем будет сильно отличаться. Так что пока они не могут полностью заменить человека-программиста, но могут сильно ускорить его работу.
Итак, самые основы вайб-кодинга. Запрос к ассистенту называется промпт. Он должен быть максимально внятным, хотя начинать можно с хоть какого-нибудь. Если вы не особо представляете, каким должно быть решение, не беда! Вместо того чтобы гуглить, спросите ИИ, он подберет варианты и выдаст их в виде хорошо прокомментированного кода.
Как и для поиска ответов на любые нетехнические вопросы, в промпте могут содержаться такие части, как:
- Роль — от лица кого вам должна отвечать нейросеть.
- Контекст — описание вашей ситуации.
- Задача — собственно, что требуется от ИИ.
- Ограничения — «направляющие» запреты на использование определенных элементов решения.
- Формат вывода — в каком виде хотите получить ответ.
- И любые другие составляющие, которые помогут повысить качество ответа.
Процесс вайб-кодинга весьма прост: выбираете ИИ-ассистент (я использовал Claude), пишете промпт, получаете ответ с кодом. В исходной задаче можно запросить не только код, но и текстовые пояснения к нему, а также несколько вариантов решения. Далее изучаете ответ, запускаете. Если вылезли ошибки, их тоже можно скормить ассистенту, он предоставит исправленный код. Если не устраивает результат — осознайте, что именно не нравится, и поведайте это ИИ. Можно запросить конкретное исправление, а можно — даже просто сомнения, недовольство, почти как с живым психологом! Терпеливый бот услужливо выдаст вам новый вариант кода. Эти итерации повторяете, пока не получите удовлетворительное решение (ну, или пока не поймете, что это вообще тупиковый путь и надо пробовать другие алгоритмы).
Теперь понятно, откуда здесь «вайб»? Разработчик думает о сути решения, а не о кодинге, «ловит вибрацию» и плывет в творческой атмосфере, не отвлекаясь на техническую реализацию.
Решаем задачу прогнозирования с помощью ИИ
Предположим, у нас есть метрика, которая с течением времени изменяется вот так:
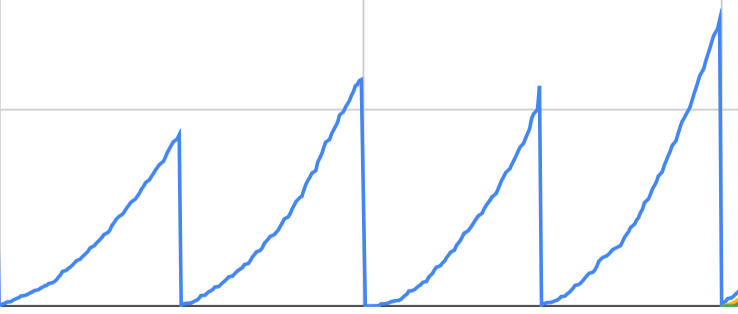
Каждый «трамплин» — это нарастающая сумма некоей величины за соответствующий квартал.
Мы хотим прогнозировать поведение этой метрики на следующий квартал. Суперточность нам не нужна, а еще мы бы хотели ограничиться языком SQL, чтобы попроще, поскромней.
Что приходит в голову при рассмотрении графика каждого квартала? На что это похоже? Да ведь это же ветвь параболы! Функция y = b × x², правда же?
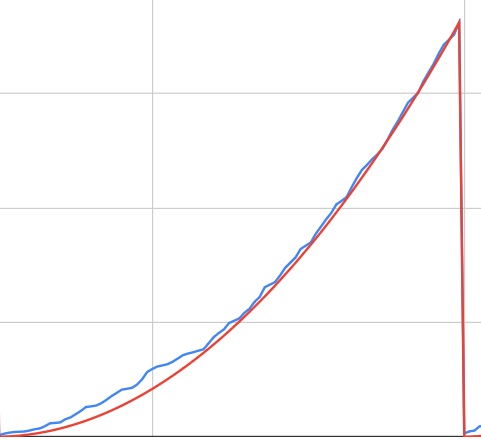
Синяя кривая — наши фактические данные, красная — график функции y = b × x².
Вдохновленный этим открытием, я затеял применить для прогнозирования аппроксимацию. Слово жутковатое, но суть удивительно проста: мы просто будем считать, что исследуемая метрика в новом квартале будет вести себя как подобранная аппроксимирующая функция.
Но как это реализовать? Я понятия не имел. Именно поэтому прибегнул к помощи нейросети.
Вайб-кодинг прогнозирования аппроксимацией
Поделюсь выжимками из моего диалога с нейроассистентом.
Я выбрал Claude 3.7 Sonnet и спросил у него без обиняков:
У меня есть временной ряд: дата и нарастающая сумма. График похож на степенную функцию. Напиши запрос на SQL ClickHouse, позволяющий подобрать параметры аппроксимирующей функции вида y = b × x^2
А он взял и ответил:
SQL-запрос для аппроксимации функцией y = b × x² в ClickHouse
Для аппроксимации временного ряда функцией вида y = b × x² в ClickHouse можно использовать более прямой подход, поскольку эта функция имеет всего один параметр b.
Если мы имеем модель y = b × x², то можно применить метод наименьших квадратов, чтобы найти оптимальное значение b. Для этой конкретной формы функции оптимальное значение b можно найти как среднее отношение y/x².
Вот SQL-запрос для ClickHouse:
WITH
-- Предполагаем, что у вас есть таблица с полями date и cumulative_sum
prepared_data AS (
SELECT
date,
cumulative_sum AS y,
-- Преобразуем дату в числовое значение (количество дней от начала отсчета)
toUInt32(date - (SELECT MIN(date) FROM your_table)) + 1 AS x
FROM your_table
WHERE cumulative_sum > 0 -- Избегаем деления на ноль
),
-- Вычисляем параметр b с помощью метода наименьших квадратов
regression AS (
SELECT
-- Для y = b × x^2, оптимальное b = avg(y/x^2)
avg(y / (x × x)) AS b
FROM prepared_data
WHERE x > 0 -- Защита от деления на ноль
)
-- Выводим результат
SELECT
b,
'y = ' || toString(b) || ' × x^2' AS formula
FROM regression;
Не забудьте заменить your_table на имя вашей таблицы с данными.
Этот запрос находит коэффициент b для функции y = b × x² и оценивает качество аппроксимации с помощью нескольких метрик.
Этот запрос действительно работал и давал примерно то, что мне нужно! Правда, коэффициент b вычислялся как среднее, из-за чего прогноз совпадал с фактом только в середине кривой, а к концу заметно превышал факт. Мне же важнее был именно конец кривой, то есть прогноз на конец квартала. Я подумал, не заменить ли среднее на медиану, но, как она там считается в ClickHouse, мне было лень искать. Я попросил ИИ:
замени среднее на медиану
Он выдал полный код, в котором отличалось CTE regression:
regression AS (
SELECT
-- Для y = b × x^2, b = median(y/x^2)
medianExact(y / (x × x)) AS b
FROM prepared_data
WHERE x > 0 -- Защита от деления на ноль
)
И добавил:
Использование медианы вместо среднего делает аппроксимацию более устойчивой к выбросам в данных. Функция medianExact() в ClickHouse вычисляет точное значение медианы, что подходит для важных расчетов, но требует больше ресурсов. Если производительность критична, можно использовать приближенную функцию median().
Так стало немного лучше, это правда приятно и удивительно, когда не нужно кодить, а только генерировать идеи и изучать результаты.
И всё же конечная точка прогноза не совпадала с фактической. Я запросил робота набросать еще несколько способов расчета коэффициента b, построил графики результатов и не удовлетворился ни одним. И только после этого до меня дошло, как задать «правильный вопрос»:
Вернемся к задаче аппроксимации. Мне нужно, чтобы конечная точка графика аппроксимирующей функции находилась там же, где конечная точка графика исходных данных. Как подобрать коэффициент b для этого?
Ассистент с готовностью ответил:
Чтобы аппроксимирующая функция вида y = b × x² проходила через конечную точку исходных данных, необходимо подобрать коэффициент b таким образом, чтобы для последней точки (x_max, y_max) выполнялось равенство:
y_max = b × (x_max)²
Отсюда получаем b = y_max / (x_max)²
Вот SQL-запрос для ClickHouse, который вычисляет такой коэффициент b:
WITH
prepared_data AS (
SELECT
date,
cumulative_sum AS y,
toUInt32(date - (SELECT MIN(date) FROM your_table)) + 1 AS x
FROM your_table
WHERE cumulative_sum > 0
),
last_point AS (
SELECT
x AS x_max,
y AS y_max
FROM prepared_data
ORDER BY date DESC
LIMIT 1
)
SELECT
y_max / (x_max × x_max) AS b,
'y = ' || toString(y_max / (x_max × x_max)) || ' × x^2' AS formula,
x_max,
y_max
FROM last_point;
Теперь графики факта и прогноза совпадали в конечной точке. Но оказалось, что при таком подходе прогноз на конец квартала рискует улететь в небеса, потому что поначалу, когда данных о текущем квартале еще недостаточно, коэффициент b оказывается сильно завышен.
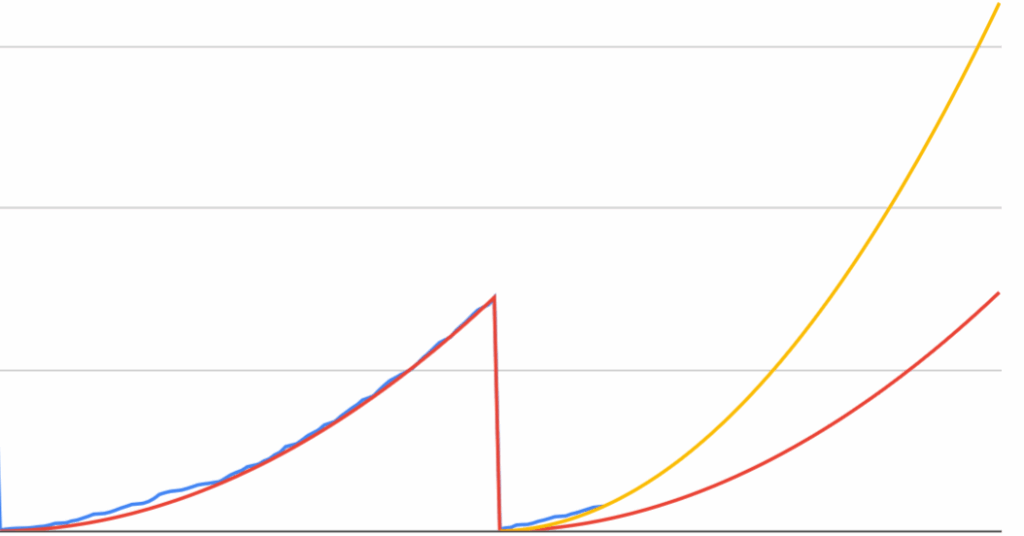
На этом графике синяя кривая — факт, красная — прогноз на последний полный квартал, желтая — прогноз на текущий, неполный квартал.
А вот как ведет себя расчетное значение коэффициента, в зависимости от момента его вычисления:
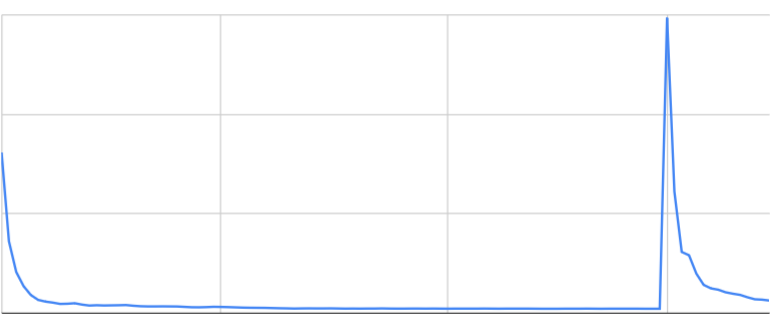
В начале квартала он огромен и быстро изменяется, но к концу первого месяца полностью «успокаивается». Исходя из этого, я решил для первой части нового квартала брать прогноз из прошлого квартала, а далее уже вычислять коэффициент. Причесав код от нейросети и реализовав эту логику, я получил вот такой итоговый запрос для прогнозирования аппроксимирующей степенной функцией:
WITH forecast_koef AS
( -- Расчет коэффициента для прошлого квартала
SELECT y / (x × x) AS b
FROM
( --
SELECT SUM(fact_data) AS y, -- исследуемая метрика
MAX(toInt32(d-q)+1) AS x -- номер последнего дня в квартале. d - дата, q - дата начала квартала
FROM datamart.fact
WHERE quarter = formatDateTime(CURRENT_DATE()-toIntervalQuarter(1), '%Y-Q%Q')
)
),
forecast_koef_current AS
( -- Расчет коэффициента для текущего квартала
SELECT y / (x × x) AS b
FROM
(
SELECT SUM(fact_data) AS y,
MAX(toInt32(d-q)+1) AS x
FROM datamart.fact
WHERE quarter = formatDateTime(CURRENT_DATE(), '%Y-Q%Q')
)
)
SELECT IFNULL(fact.quarter, f.quarter) AS quarter,
IFNULL(fact.d, f.d) AS d,
fact,
forecast
FROM
( -- фактические данные. d - дата, fact_data - исследуемая метрика
SELECT quarter, d,
SUM(fact_data) AS fact_data
FROM datamart.fact
GROUP BY ALL
) AS fact
FULL OUTER JOIN
( -- прогнозные данные
SELECT number + 1 AS x, -- номер дня
toStartOfQuarter(now())+toIntervalDay(number) AS d, -- день
formatDateTime(d, '%Y-Q%Q') quarter, -- квартал
IF(CURRENT_DATE() >= date_trunc('quarter', CURRENT_DATE()) + INTERVAL 1 MONTH,
(SELECT b FROM forecast_koef_current), -- коэф. для текущего квартала
(SELECT b FROM forecast_koef) -- коэф. для прошлого квартала
) AS b,
b × (x × x) AS forecast -- прогноз аппроксимацией
-- генератор дат на текущий квартал
FROM numbers(dateDiff('day',
toStartOfQuarter(now()),
toStartOfQuarter(now()) + INTERVAL 3 MONTH - INTERVAL 1 DAY
) + 1)
) AS f ON f.d = fact.d
Резюме
В этой статье я совместил две темы в одном кейсе:
- Прогнозирование на SQL степенной аппроксимирующей функцией вида y = b × x2. Главная задача — выбрать способ вычисления коэффициента b (как среднее, медиана или последнее значение временного ряда).
- Вайб-кодинг — не только способ программирования, но и инструмент поиска лучшего технического решения. Рассмотрели выжимку из диалога разработчика и нейросети в рамках решения задачи прогнозирования.